문제 요약
https://www.acmicpc.net/problem/12015
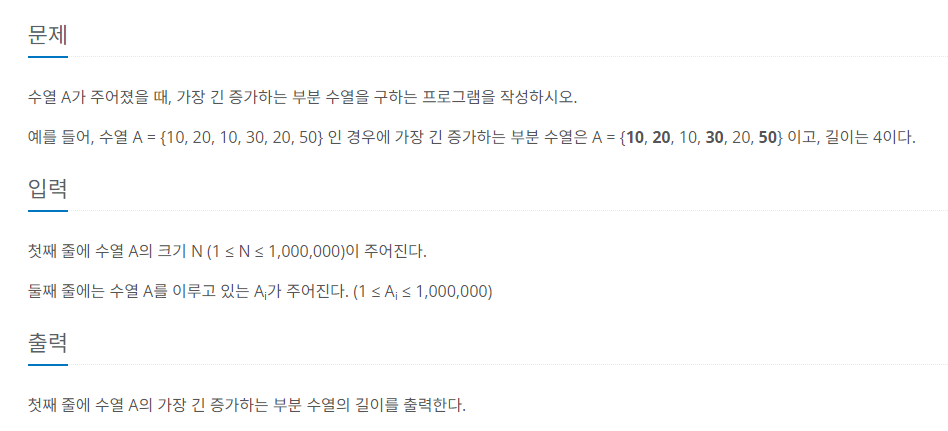
수열에서 가장 긴 증가하는 부분 수열의 길이를 출력하는 문제.
접근
가장 긴 증가하는 부분 수열을 구하기 위해서는 완전탐색, DP, 이분탐색을 사용할 수 있다.
완전탐색의 시간복잡도는 O(2^n), DP의 시간복잡도는 O(n^2), 이분탐색의 시간복잡도는 O(nlogn)라고 한다.
문제 조건에서 수열의 크기는 최대 1,000,0000이기 때문에 이분탐색을 선택했다.
스택에 증가하는 수열을 저장했다.
새로운 값이 stack[-1]보다 크면 스택의 가장 위에 넣어주고 작으면 이분탐색을 통해 넣을 위치를 찾아주었다.
새로운 값과 stack[-1]이 같으면 무시해주었다.
스택에서 이분탐색을 할 때 target과 일치하는 값을 찾는 것이 아니라, target보다 큰 값들 중 최소값을 찾아야한다.
따라서
target 값이 stack[mid]보다 작으면 탐색 범위를 mid를 포함한 (srt, mid)로,
target 값이 stack[mid]보다 크면 탐색 범위를 (mid+1, end)로 설정했다.
두 값이 같을 때는 인덱스 값을 mid로 return해주었다.
srt == end 일 때 while문에서 빠져나와 end 값을 반환하면서 이분탐색이 끝난다.
코드
import sys
input = sys.stdin.readline
def bin_search(srt, end, target):
while srt < end:
mid = (srt + end) // 2
if target > stack[mid]:
srt = mid + 1
elif target < stack[mid]:
end = mid
else:
return mid
return end
n = int(input())
arr = list(map(int, input().split()))
stack = [arr[0]]
for i in range(1, n):
if arr[i] > stack[-1]:
stack.append(arr[i])
elif arr[i] < stack[-1]:
stack[bin_search(0, len(stack) - 1, arr[i])] = arr[i]
print(len(stack))다른 풀이
위 코드보다 시간복잡도, 공간복잡도가 훨씬 적은 코드가 있어서 봤더니 bisect라는 라이브러리를 사용한 코드였다.
bisect를 사용하면 시간복잡도를 훨씬 줄일 수 있다고 한다.
bisect_left(arr, target, srt, end)
target 값이 삽입되어야 할 가장 왼쪽 인덱스를 반환한다.
bisect(arr, target, srt, end) == bisect_right(arr, target, srt, end)
target 값이 삽입되어야 할 가장 오른쪽 인덱스를 반환한다.
arr에 target이 존재하지 않는다면 이 둘의 결과값은 동일하다.
반면 이미 arr에 target이 존재할 경우에는
bisect_left는 이미 존재하는 target 값들 중 가장 왼쪽 인덱스를, bisect_right는 target이 새로 삽입될 위치를 반환한다.
두 bisect 모두 정렬되어 있는 리스트에서만 사용할 수 있다.
참고) https://gr-st-dev.tistory.com/864#google_vignette
bisect를 이 문제에 적용한 풀이
import sys
import bisect
input = sys.stdin.readline
n = int(input())
arr = list(map(int, input().split()))
stack = [arr[0]]
for i in range(1, n):
if arr[i] > stack[-1]:
stack.append(arr[i])
else:
stack[bisect.bisect_left(stack, arr[i])] = arr[i]
print(len(stack))'코테 준비' 카테고리의 다른 글
| [프로그래머스] 주차 요금 계산 (0) | 2024.03.07 |
|---|---|
| [프로그래머스] 둘만의 암호 (Python) (0) | 2024.03.07 |
| [프로그래머스] 110 옮기기 (0) | 2024.02.29 |
| [프로그래머스] 교점에 별 만들기 (1) | 2024.02.29 |
| [프로그래머스] 혼자 놀기의 달인 (2) | 2024.02.29 |


